clase ··#3
"En esta clase de cálculo, el tema que estamos viendo ahora es el límite de una constante. Siento que la materia en general es bastante desafiante, ya veces siento que no profundizamos lo suficiente en cada tema. Apenas estamos comenzando a entender uno cuando ya Estamos avanzando al siguiente. Sé que debemos ser autodidactas, pero el tiempo se me va tan rápido que a menudo siento que no me alcanza. Tal vez debería organizarme mejor para poder dedicarle más tiempo. para nosotros, los estudiantes, se complica un poco. Y digo 'nosotros' porque mis compañeros están pasando por lo mismo que yo."
conocimiento consultado:
Trigonometría básica
Si conocemos dos lados de un triángulo rectángulo, podemos calcular el otro lado aplicando el teorema de Pitágoras. Sin embargo, en ocasiones no conocemos dos lados, pero sí conocemos uno de los otros dos ángulos no rectos. En estos casos es cuando utilizamos el seno y el coseno.
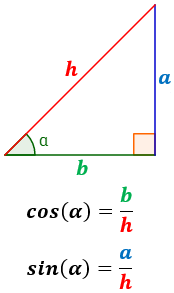
- El coseno de un ángulo α se define como el cociente del lado contiguo al ángulo α y la hipotenusa.
- El seno de α se define como el cociente del lado opuesto al ángulo α y la hipotenusa.
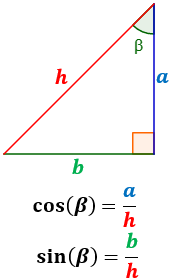
Nota: si cambiamos de ángulo, cambian los numeradores:
Normalmente, para referirnos al seno de α podemos escribir sin(α), sen(α) ó seno(α). Y para el coseno, cos(α) ó coseno(α).
La tangente del ángulo α es el cociente del seno y del coseno de dicho ángulo:
La tangente es el cociente del lado opuesto y del lado contiguo.
La tangente del ángulo α puede escribirse como tan(α) y como tg(α), entre otras.
Ejemplos de aplicación
Problema 1
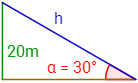
Se desea sujetar un poste de 20 metros de altura con un cable que parte de la parte superior del mismo hasta el suelo de modo que forme un ángulo de 30º.
Calcular el precio del cable si cada metro cuesta 12$.
Solución:
Como conocemos el lado opuesto, a=20m, utilizamos el seno para calcular la hipotenusa del triángulo:
Sustituimos el ángulo y el lado:
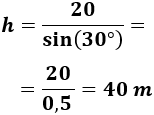
https://www.funciones.xyz/limites-trigonometricos/
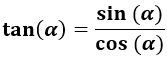
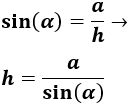

Comentarios
Publicar un comentario