Título: máximos y mínimos
"En esta última clase, después de haber revisado los conceptos de máximo y mínimo, me resultó un poco inquietante que el profesor dedicara tiempo a un tema nuevo. Si bien agradezco el adelanto, siento que esto generó cierta confusión en mí y en mis compañeros. En lugar de ello, creo que hubiera sido más beneficioso consolidar los conocimientos adquiridos durante el cuatrimestre y que la introducción al nuevo tema fuera más breve. Espero poder comprender mejor este nuevo concepto y confío en que el profesor priorizará nuestro aprendizaje por encima de simplemente cubrir el temario en el próximo cuatrimestre."
Conocimiento consultado: Antes que todo establezcamos cierta notación alterna para las derivadas de una función  .
.
La razón de establecer notaciones alternas para el mismo concepto, es porque hay ocasiones en que los desarrollos son muy grandes o complicados, y es necesario para que sea más práctico que se hagan menos extensas las notaciones, ya que aquí lo importante es que sigan representando el mismo concepto.
La primer derivada de una función tiene las tres notaciones que tenemos aquí:
y la segunda derivada de una función (la derivada de la derivada), tiene las siguientes notaciones alternas:
en este caso por términos de claridad ocuparemos para la primer derivada, a la notación 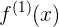 , y para la segunda derivada
, y para la segunda derivada 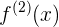 .
.
Una vez establecida la notación que usaremos, comentemos acerca de ciertas características que podemos estudiar de las funciones.
Hablando de forma más precisa, conozcamos los criterios que nos informan dónde una función adquiere su máximo o mínimo valor posible dentro de una región establecida, razón por la cual se llaman máximo o mínimo relativos.
Repasa los máximos y mínimos de funciones con clases particulares matematicas de Superprof.
Extremos relativos
Antes que todo identifiquemos el tipo de punto que deseamos localizar, en términos simples se trata de puntos donde una función adquiere un máximo o mínimo valor posible, esto es en comparación a los puntos de un entorno cercano a ellos, a este tipo de puntos los llamaremos extremos relativos.
Si 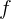 es una función derivable en
es una función derivable en 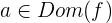 , entonces
, entonces  es un extremo relativo o local si:
es un extremo relativo o local si:
Máximos relativos
Si 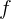 es una función derivable en
es una función derivable en 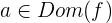 , entonces
, entonces  es un máximo relativo o local si:
es un máximo relativo o local si:
Mínimos relativos
Si 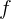 es una función derivable en
es una función derivable en 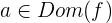 , entonces
, entonces  es un mínimo relativo o local si:
es un mínimo relativo o local si:
Cálculo de máximos y mínimos
Consideremos a la siguiente función 
Para hallar los extremos locales seguiremos los siguientes pasos:
1Hallamos la primera derivada de la función y calculamos sus raíces.
Primero la derivada de la función

Ahora sus raíces, resolviendo la ecuación

Entonces sus raíces son

2Realizamos la segunda derivada, y calculamos el signo que toman en ella las raíces.
Calculemos la segunda derivada de la función

Evaluemos las raíces obtenidas en la segunda derivada
 ,
,  en
en  la función tiene un máximo relativo
la función tiene un máximo relativo
 ,
,  en
en  la función tiene un mínimo relativo
la función tiene un mínimo relativo
3Calculamos la imagen (en la función) de los extremos relativos.
 ,
, en
en  la gráfica de la función tiene un máximo relativo
la gráfica de la función tiene un máximo relativo
 ,
,  en
en  la gráfica de la función tiene un mínimo relativo
la gráfica de la función tiene un mínimo relativo
¿Vives en la capital? ¡Échale un ojo a nuestras clases particulares matematicas madrid!
Estudio de los extremos relativos a partir del crecimiento
Si ya hemos estudiado el crecimiento y decrecimiento de una función habrá:
- Un máximo en el punto de la función cuando esta pasa de creciente
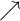 a decreciente
a decreciente  .
. - Un mínimo en el punto de la función cuando esta pasa de decreciente
 a creciente
a creciente 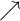 .
.
Ejemplo:
Consideremos a la siguiente función 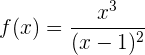
Para hallar los extremos locales seguiremos los siguientes pasos:
1Hallamos el dominio de la función, la primera derivada y calculamos sus raíces.
Primero el dominio de la función
Busquemos los puntos donde se indetermina la función, es decir, valores donde 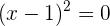
https://www.superprof.es/apuntes/escolar/matematicas/calculo/funciones/maximos-y-minimos.html
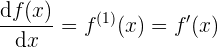
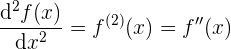
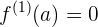

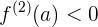
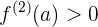

Comentarios
Publicar un comentario