DIARIO # 4

TEMA: Definición de una función

"Esta clase me pareció un poco más interesante, aunque todavía encuentro un poco confuso el concepto de 'x' y 'y'. Creo que profundizando más en el tema y consultando videos y otras fuentes confiables de información, se me irá haciendo más fácil dominar las matemáticas."

"Hablo de las matemáticas en general, ya que siento que me cuesta un poco recordar los pasos. Mientras el profesor explica, me resulta fácil entender, pero una vez que lo intento por mi cuenta, tiendo a olvidarlo."

CONOCIMIENTO CONSULTADO:

¿Qué es una función en matemáticas?

En este artículo explicamos qué es una función en matemáticas, cómo se simboliza, las formas de clasificación y ejemplos de funciones.

Índice

• ¿Qué es una función?
• Simbología
• Ejemplos
• Tipos de funciones
• Definición formal de función
• Preguntas frecuentes                                                                                                                                                                                                ¿Qué es una función?

Una función es una regla que hace corresponder a cada elemento de un conjunto, llamado dominio, un único elemento de otro conjunto, llamado codominio.

Hablamos de función o relación funcional cuando se nos presentan relaciones entre dos conjuntos de elementos, en las que a cada elemento del primer conjunto se le hace corresponder únicamente un elemento del otro conjunto. Por ejemplo, a cada persona le corresponde una edad, a cada estado le corresponde un gobernador, a cada palabra le corresponde una letra inicial, etc.

Ahora bien, no todas las relaciones entre conjuntos son funciones. Por ejemplo, la relación "es padre de" entre personas no es una función, ya que una persona puede tener más de un hijo, y algunas personas pueden no tener hijos.

En matemáticas es común trabajar con relaciones de dos magnitudes variables donde una depende de la otra. Por ejemplo, el área A de un círculo depende de su radio, y está dada por la expresión A=πr2. La relación entre estas magnitudes es una función, porque a cada valor de radio le corresponde un único valor de área. Matemáticamente podemos precisar aún más el concepto de función mediante la siguiente definición.

Definición: una función f es una regla que asigna a cada elemento x de un conjunto A, un único elemento y de un conjunto B. El conjunto A se llama dominio de f. El conjunto B se llama codominio y el conjunto de las y en B se denomina rango de f. 

Dada una función f, el elemento y del rango que corresponde a un x escogido en el dominio es el valor de la función en x, o la imagen de x, que se denota por f(x). Este símbolo se lee "f de x" o "f en x" y queda claro que y=f(x). El valor de y depende de la elección de x, por lo que se le denomina variable dependiente; a x se la llama variable independiente.

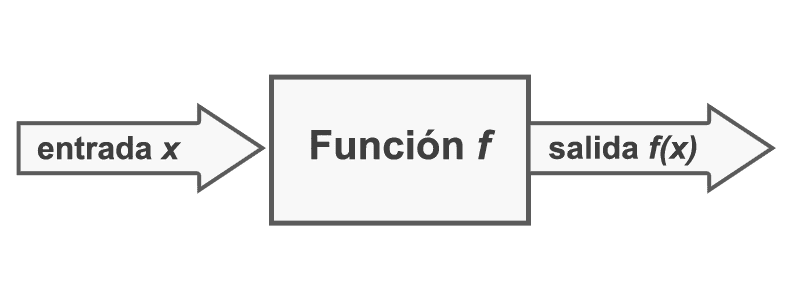
Es útil considerar una función como una máquina. Si x está en el dominio de la función f, entonces cuando x entra a la máquina, es aceptada como entrada y la máquina produce una salida y=f(x) de acuerdo con la regla de la función. La entrada es la variable independiente y la salida es la variable dependiente.

Otra forma de presentar a una función es mediante un diagrama de flechas. Cada flecha conecta un elemento de A con su correspondiente en B. En el siguiente gráfico se observa que x está relacionado con f(x) y a está relacionado con f(a). El conjunto A suele llamarse conjunto de partida y el conjunto B conjunto de llegada.

Diagrama de una función

Por ejemplo, la regla para elevar al cuadrado un número está dada por la ecuación $f(x)=x^2$ o $y=x^2\mathrm{.}$ El valor de f en $x=2$ se obtiene de sustituir $x$ en la fórmula:

$f(2)=(2{)}^2=4$

Así, al elemento $x=2$ le corresponde el elemento $y=4$ según la regla de la función f.

A partir de la definición podemos decir que características de una función son:

• Existencia: para cada elemento del dominio, debe existir una imagen en el codominio. No puede haber elementos en el dominio que no tengan una imagen asociada.
• Unicidad: cada elemento del dominio debe tener una única imagen en el codominio. Esto significa que no puede haber dos imágenes diferentes para un mismo elemento del dominio.

Los elementos de una función son:

• Dominio: es el conjunto de todos los posibles valores de entrada para los cuales la función está definida.
• Codominio: es el conjunto de llegada de la función, el cual contiene a todos los valores de salida.
• Rango: es el conjunto de todos los valores de salida y está dentro del codominio. El rango no es necesariamente igual al codominio.
• Regla de correspondencia: es aquella que dicta cómo se relacionan los elementos del dominio con los del codominio. Puede ser una expresión algebraica, una tabla, un gráfico o una descripción verbal. Véase formas de representar una función.

El dominio y el rango de una función pueden ser cualesquiera conjuntos de objetos, pero en matemáticas, especialmente en cálculo, suelen ser conjuntos de números reales. A las funciones de este tipo se les llama funciones reales de variable real.

Simbología

Las funciones se denotan habitualmente con el símbolo f(x), donde f es el nombre de la función y x es el valor de entrada. En contextos diferentes de matemáticas suelen usarse para las funciones los símbolos como F, G, H, f, g, h, p, q, etc. Para las variables dependientes o independientes se utilizan las letras minúsculas r, s, t, u, v, w, x, y, z.

Así, una función podría escribirse como w=G(z) o v=h(t). Por ejemplo, en la función $A=\pi r^2$ identificamos que la variable independiente es r y la dependiente es A. 

La simbología habitual utilizada en análisis matemático para explicitar el dominio y el codominio es:

$$\begin{gathered} f:A\to B \\ x\to f(x) \end{gathered}$$

que se lee como "f es una función definida de A en B, al elemento x le corresponde f(x)".

Por ejemplo, la función $f(x)=x^2$ se expresa así:

$$\begin{gathered} f:\mathbb{R}\to \mathbb{R} \\ x\to x^2 \end{gathered}$$

Ejemplos

A continuación, veremos algunos ejemplos de funciones matemáticas:

1. A todos los números reales no negativos se le puede extraer su raíz cuadrada. La función $f(x)=\sqrt{x}$ toma un número x y devuelve su raíz cuadrada.
2. La función $y=x^2$ relaciona a cada número real x con su cuadrado y.
3. La función $g(x)=\mathrm{\mid }x\mathrm{\mid }$ asigna a cada número real su valor absoluto.
4. El área de un círculo depende de su radio. La fórmula $A=\pi r^2$ nos da el área A de un círculo de radio r.
5. La función $y=\frac{1}{x}$ hace corresponder a cada número real diferente de cero su inverso multiplicativo, también llamado recíproco.
6. La función $h(x)=\ln (x)$ asigna a cada número real positivo x su logaritmo natural.
7. Todo número real posee una raíz cúbica, la función $y=\sqrt[3]{x}$ relaciona a cada número x con su raíz cúbica y.
8. La función descrita por la fórmula $v=\cos (u)$ asigna a cada número real u el valor de su coseno trigonométrico.
9. El área de un cuadrado depende de la longitud de su lado, así, si el lado es $x$, el área del cuadrado está dada por la función $A(x)=x^2\mathrm{.}$
10. Todo número real tiene un doble, el cual se obtiene multiplicándolo por 2. La función $f(x)=2x$ toma como entrada un número x y arroja como salida su doble.

https://www.bing.com/search?PC=X847&FORM=X847DF&q=definicion+de+la+funcion